Astronomía Esférica, o Astronomía de posición. Trigonometría esférica
La Astronomía Esférica, o Astronomía de posición, se refiere fundamentalmente a las direcciones en las cuales los astros son vistos, sin tener en cuenta sus distancias. Es conveniente expresar esas direcciones en términos de las posiciones sobre la superfície de una esfera, la Esfera Celeste. Esas posiciones son medidas únicamente en ángulos. De esa forma, el radio de la esfera, que es totalmente arbitrario, no entra en las ecuaciones.
Definiciones básicas:
Si un plano pasa por el centro de una esfera, la dividirá en dos hemisferios idénticos, a lo largo de un círculo máximo. Cualquier plano que corta la esfera sin pasar por su centro la intercepta en un círculo menor.
Cuando dos círculos máximos se interceptan en un punto, forman entre si un ángulo esférico. La medida de un ángulo esférico es igual a la medida del ángulo plano entre las tangentes de los dos arcos que lo forman.
Un ángulo esférico también es medido por el arco esférico correspondiente, que es el arco de un círculo máximo contenido entre los dos lados del ángulo esférico y distantes 90° de su vértice. La medida de un arco esférico, a su vez, es igual al ángulo que subtiende desde el centro de la circunferencia.
Triángulos esféricos.
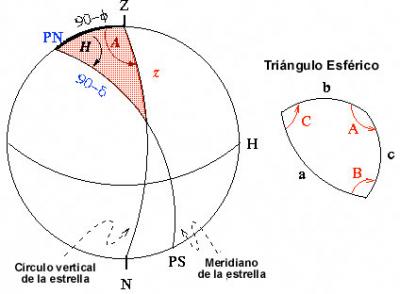
Un triángulo esférico no es cualquier figura de tres lados sobre la esfera; sus lados deben ser arcos de círculos máximos, o sea, arcos esféricos. Denotamos a los ángulos de un triángulo esférico por letras mayúsculas (A,B,C), y a sus lados por letras minúsculas (a,b,c).
Propiedades de los triángulos esféricos
1) La suma de los ángulos de un triángulo esférico es siempre mayor que 180°, y menor que 270°, y no es constante, dependiendo del triángulo. De hecho, el valor de la suma de los ángulos por encima de 180° es directamente proporcional al área del triángulo.
2) La suma de los lados de un triángulo esférico es mayor que cero y menor que 180°.
3) Los lados mayores están opuestos a los ángulos mayores del triángulo.
4) La suma de dos lados del triángulo es siempre mayor que el tercer lado, y la diferencia es siempre menor.
5) Cada uno de los lados del triángulo es menor que 180°, y esto se aplica tambien a los ángulos.
Solución de triángulos esféricos:
Al contrario de la trigonometría plana, no es suficiente con conocer dos ángulos para resolver el triángulo. Es siempre necesario conocer como mínimo tres elementos: o tres ángulos, o tres lados, o dos lados y un ángulo, o un lado y dos ángulos.
Las fórmulas principales para la solución de los triángulos esféricos son:
fórmula de los cosenos:
cosa = cosb cosc + senb senc cosA
y la fórmula de los senos:
sena/senA = senb/senB = senc/senC
